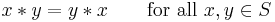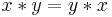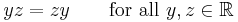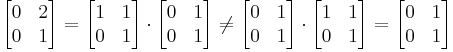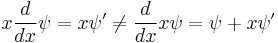Commutative property
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. The commutativity of simple operations, such as multiplication and addition of numbers, was for many years implicitly assumed and the property was not named until the 19th century when mathematics started to become formalized. By contrast, division and subtraction are not commutative.
Contents |
Common uses
The commutative property (or commutative law) is a property associated with binary operations and functions. Similarly, if the commutative property holds for a pair of elements under a certain binary operation then it is said that the two elements commute under that operation.
In group and set theory, many algebraic structures are called commutative when certain operands satisfy the commutative property. In higher branches of mathematics, such as analysis and linear algebra the commutativity of well known operations (such as addition and multiplication on real and complex numbers) is often used (or implicitly assumed) in proofs.[1][2][3]
Mathematical definitions
The term "commutative" is used in several related senses.[4][5]
1. A binary operation ∗ on a set S is called commutative if:
An operation that does not satisfy the above property is called noncommutative.
2. One says that x commutes with y under ∗ if:
3. A binary function 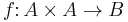 is called commutative if:
is called commutative if:
History and etymology
Records of the implicit use of the commutative property go back to ancient times. The Egyptians used the commutative property of multiplication to simplify computing products.[6][7] Euclid is known to have assumed the commutative property of multiplication in his book Elements.[8] Formal uses of the commutative property arose in the late 18th and early 19th centuries, when mathematicians began to work on a theory of functions. Today the commutative property is a well known and basic property used in most branches of mathematics.
The first recorded use of the term commutative was in a memoir by François Servois in 1814,[9][10] which used the word commutatives when describing functions that have what is now called the commutative property. The word is a combination of the French word commuter meaning "to substitute or switch" and the suffix -ative meaning "tending to" so the word literally means "tending to substitute or switch." The term then appeared in English in Philosophical Transactions of the Royal Society in 1844.[9]
Related properties
Associativity
The associative property is closely related to the commutative property. The associative property of an expression containing two or more occurrences of the same operator states that the order operations are performed in does not affect the final result, as long as the order of terms doesn't change. In contrast, the commutative property states that the order of the terms does not affect the final result.
Symmetry
Some forms of symmetry can be directly linked to commutativity. When a commutative operator is written as a binary function then the resulting function is symmetric across the line y = x. As an example, if we let a function f represent addition (a commutative operation) so that f(x,y) = x + y then f is a symmetric function, which can be seen in the image on the right.
For relations, a symmetric relation is analogous to a commutative operation, in that if a relation R is symmetric, then 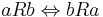 .
.
Examples
Commutative operations in everyday life
- Putting on socks resembles a commutative operation, since which sock is put on first is unimportant. Either way, the end result (having both socks on), is the same.
- The commutativity of addition is observed when paying for an item with cash. Regardless of the order the bills are handed over in, they always give the same total.
Commutative operations in mathematics
Two well-known examples of commutative binary operations are:[4]
- The addition of real numbers, which is commutative since
-
- For example 4 + 5 = 5 + 4, since both expressions equal 9.
- The multiplication of real numbers, which is commutative since
-
- For example, 3 × 5 = 5 × 3, since both expressions equal 15.
- Further examples of commutative binary operations include addition and multiplication of complex numbers, addition and scalar multiplication of vectors, and intersection and union of sets.
Noncommutative operations in everyday life
- Concatenation, the act of joining character strings together, is a noncommutative operation. For example
- Washing and drying clothes resembles a noncommutative operation; washing and then drying produces a markedly different result to drying and then washing.
- Rotating a book 90° around a vertical axis then 90° around a horizontal axis produces a different orientation than when the rotations are performed in the opposite order.
- The twists of the Rubik's Cube are noncommutative. This can be studied using group theory.
Noncommutative operations in mathematics
Some noncommutative binary operations are:[11]
- Subtraction is not commutative since
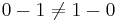
- Division is noncommutative since
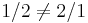
- Matrix multiplication is noncommutative since
- The vector product (or cross product) of two vectors in three dimensions is anti-commutative, i.e., b × a = −(a × b).
Mathematical structures and commutativity
- A commutative semigroup is a set endowed with a total, associative and commutative operation.
- If the operation additionally has an identity element, we have a commutative monoid
- An abelian group, or commutative group is a group whose group operation is commutative.[2]
- A commutative ring is a ring whose multiplication is commutative. (Addition in a ring is always commutative.)[12]
- In a field both addition and multiplication are commutative.[13]
Non-commuting operators in quantum mechanics
In quantum mechanics as formulated by Schrödinger, physical variables are represented by linear operators such as x (meaning multiply by x), and d/dx. These two operators do not commute as may be seen by considering the effect of their products x(d/dx) and (d/dx)x on a one-dimensional wave function ψ(x):
According to the uncertainty principle of Heisenberg, if the two operators representing a pair of variables do not commute, then that pair of variables are mutually complementary, which means they cannot be simultaneously measured or known precisely. For example, the position and the linear momentum of a particle are represented respectively (in the x-direction) by the operators x and (ħ/i)d/dx (where ħ is the reduced Planck constant). This is the same example except for the constant (ħ/i), so again the operators do not commute and the physical meaning is that the position and linear momentum in a given direction are complementary.
See also
- Anticommutativity
- Binary operation
- Commutant
- Commutative diagram
- Commutative (neurophysiology)
- Commutator
- Distributivity
- Particle statistics (for commutativity in physics)
Notes
References
Books
- Axler, Sheldon (1997). Linear Algebra Done Right, 2e. Springer. ISBN 0-387-98258-2.
- Abstract algebra theory. Covers commutativity in that context. Uses property throughout book.
- Goodman, Frederick (2003). Algebra: Abstract and Concrete, Stressing Symmetry, 2e. Prentice Hall. ISBN 0-13-067342-0.
- Abstract algebra theory. Uses commutativity property throughout book.
- Gallian, Joseph (2006). Contemporary Abstract Algebra, 6e. Boston, Mass.: Houghton Mifflin. ISBN 0-618-51471-6.
- Linear algebra theory. Explains commutativity in chapter 1, uses it throughout.
Articles
- http://www.ethnomath.org/resources/lumpkin1997.pdf Lumpkin, B. (1997). The Mathematical Legacy Of Ancient Egypt - A Response To Robert Palter. Unpublished manuscript.
- Article describing the mathematical ability of ancient civilizations.
- Robins, R. Gay, and Charles C. D. Shute. 1987. The Rhind Mathematical Papyrus: An Ancient Egyptian Text. London: British Museum Publications Limited. ISBN 0-7141-0944-4
- Translation and interpretation of the Rhind Mathematical Papyrus.
Online resources
- Krowne, Aaron, Commutative at PlanetMath., Accessed 8 August 2007.
- Definition of commutativity and examples of commutative operations
- Weisstein, Eric W., "Commute" from MathWorld., Accessed 8 August 2007.
- Explanation of the term commute
- Yark. Examples of non-commutative operations at PlanetMath., Accessed 8 August 2007
- Examples proving some noncommutative operations
- O'Conner, J J and Robertson, E F. MacTutor history of real numbers, Accessed 8 August 2007
- Article giving the history of the real numbers
- Cabillón, Julio and Miller, Jeff. Earliest Known Uses Of Mathematical Terms, Accessed 22 November 2008
- Page covering the earliest uses of mathematical terms
- O'Conner, J J and Robertson, E F. MacTutor biography of François Servois, Accessed 8 August 2007
- Biography of Francois Servois, who first used the term